DELSE

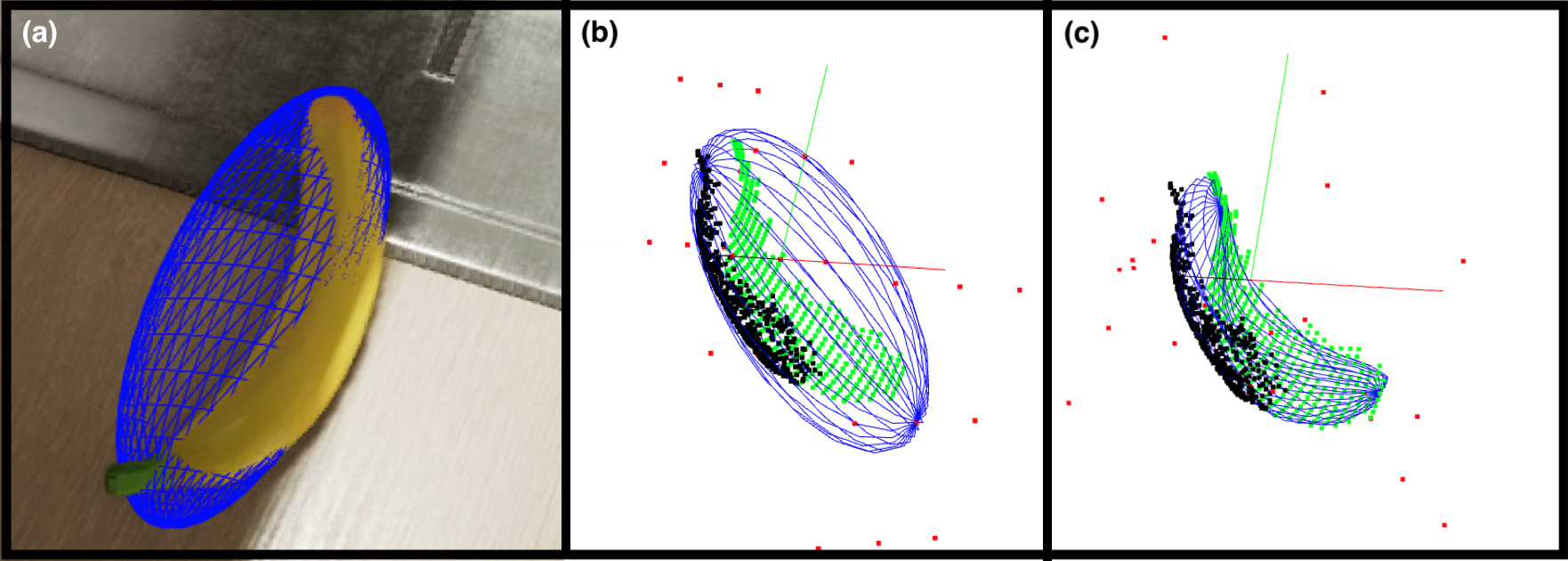
It is often important for robots to know the location and shape of objects. However, this task can be a bit tricky! Many times robots can only obtain partial observations due to self-occlusions or occlusions in the scene. In this project (which is approximately equivalent to half of an undergraduate senior- year research project, with the other half being the learned descriptors project), I have attempted to compute continuous and differentiable object shape representations from partial observations.

Past works have attempted to learn object shapes from incomplete data via vast training datasets. While effective for previously known and well defined objects (e.g., cars and bottles), these methods could fall short when estimating shapes of arbitrary objects (e.g. rocks or deformed packages). In this work I have leveraged past work on computing ellipsoid shape estimates to objects and designed a method that further improves on such coarse estimates by deforming the prior ellipsoids to tightly fit partial observations while retaining a reasonable volume and without relying on prior shape or semantic knowledge.

That’s it, in a nutshell! The method in some more detail is outlined in the video and described in much much more detail is described in the PDF 🤖.